2º F - 3º Bimestre - Aula 4

 

2º F - 3º Bimestre  - Aula 4

Velocidade de propagação das ondas

Como não transportam matéria em seu movimento, é previsível que as ondas se desloquem com velocidade contínua, logo estas devem ter um deslocamento que valide a expressão:

Que é comum aos movimentos uniformes, mas conhecendo a estrutura de uma onda:

Podemos fazer que ΔS=λ e que Δt=T. Assim:

Esta é a equação fundamental da Ondulatória, já que é valida para todos os tipos de onda.

É comum utilizar-se frequências na ordem de kHz (1quilohertz = 1000Hz) e de MHz (1megahertz = 1000000Hz)

Exemplo:

(1) Qual a frequência de ondas, se a velocidade desta onde é de 195m/s, e o seu comprimento de onda é de 1cm?

1cm=0,01m

 

Exercícios

1- (FAMEMA-SP) Com o objetivo de simular as ondas no mar, foram geradas, em uma cuba de ondas de um laboratório, as ondas bidimensionais representadas na figura, que se propagam de uma região mais funda (região 1) para uma região mais rasa (região 2).

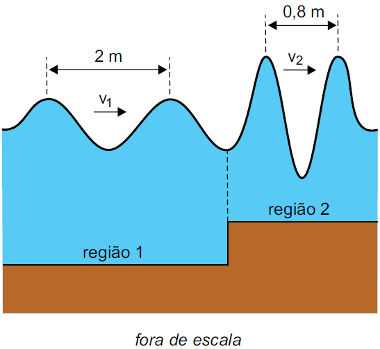
Sabendo que, quando as ondas passam de uma região para a outra, sua frequência de oscilação não se altera e considerando as medidas indicadas na figura, é correto afirmar que a razão entre as velocidades de propagação das ondas nas regiões 1 e 2 é igual a:

a) 1,6.

b) 0,4.

c) 2,8.

d) 2,5.

e) 1,2.

2-O som mais grave que o ouvido humano é capaz de ouvir possui comprimento de onda igual a 17 m. Sendo assim, determine a mínima frequência capaz de ser percebida pelo ouvido humano.

Dados: Velocidade do som no ar = 340 m/s

a) 10 Hz

b) 15 Hz

c) 17 Hz

d) 20 Hz

e) 34 Hz 

3-- . O gráfico abaixo representa uma onda que se propaga com velocidade igual a 300m/s.

Determine:

a) a amplitude da onda;

b) o comprimento de onda;

c) a frequência;

d) o período